nLab Gepner model
Context
Quantum field theory
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Contents
Idea
A Gepner model (Gepner 87) is a rational 2d SCFT which is a tensor product of super-minimal model CFT.
This means that Gepner models are “non-geometric string vacua” in that they do not arise as sigma-models with target space a smooth manifold. Indeed the Gepner models appear as the limiting cases of sigma-models with target space a 6d Calabi-Yau manifold at singular points in the moduli space of the CY target: the flop transition.
As such the Gepner models are directly analogous to the purely algebraically defined non-classical fibers in the Connes-Lott-Chamseddine-Barrett model (it is a “2-spectral triple”-analog of the spectral triples in the Connes-Lott model, see there) and, accordingly, plays a central role in string phenomenology (for review see e.g. Reppel 07).
The Gepner models are a basic building block for rational conformal field theory.
Properties
Boundary states
All the known rational boundary states for Gepner models can be regarded as permutation branes.
(Enger-Recknagel-Roggenkamp 05)
Phenomenology
Discussion of string phenomenology of intersecting D-brane models KK-compactified with non-geometric fibers such that the would-be string sigma-models with these target spaces are in fact Gepner models (in the sense of Spectral Standard Model and String Compactifications) is in (Dijkstra-Huiszoon-Schellekens 04a, Dijkstra-Huiszoon-Schellekens 04b):
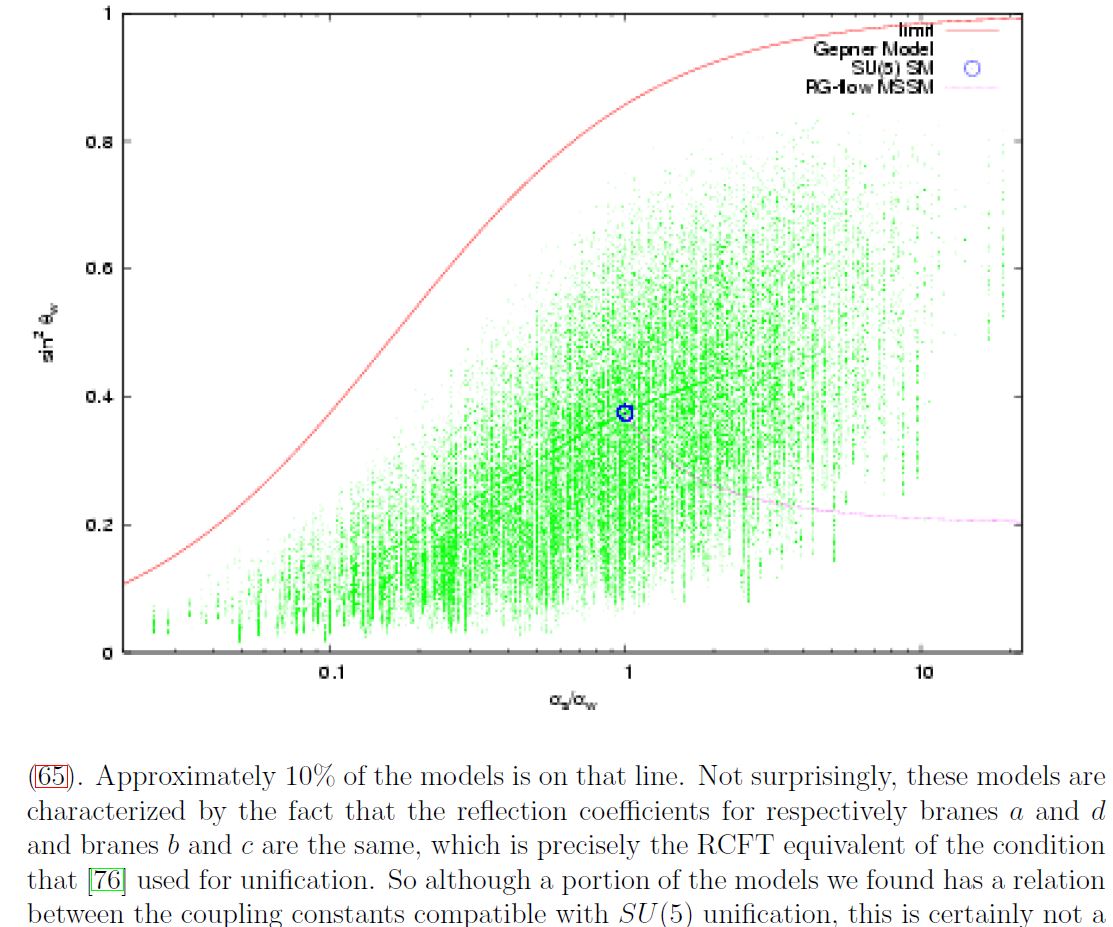
A plot of standard model-like coupling constants in a computer scan of Gepner model-KK-compactification of intersecting D-brane models according to Dijkstra-Huiszoon-Schellekens 04b.
The blue dot indicates the couplings in -GUT theory. The faint lines are NOT drawn by hand, but reflect increased density of Gepner models as seen by the computer scan.
Related concepts
References
The original article is
- Doron Gepner, Space-time supersymmetry in compactified string theory and superconformal models, Nucl. Phys. B 296 (1987) 757 [doi:10.1016/0550-3213(88)90397-5]
Lecture notes include:
- Doron Gepner, Lectures On String Theory, 1989 [pdf, spire:277718/]
Further discussion in
- Maximilian Kreuzer, Heterotic Gepner Models and Related Geometries, in Fundamental Interactions, pp. 335-362 World Scientific (2009) (arXiv:0904.4467, doi:10.1142/9789814277839_0019)
See also the references at flop transition for more.
Review of application in string phenomenology includes
- Christian Reppel, Phenomenological Aspects of Gepner Models, 2007 (pdf)
D-branes in string theory vacua defined by Gepner model SCFTs are discussed, via boundary conformal field theory in
-
Jürgen Fuchs, Christoph Schweigert, J. Walcher, Projections in string theory and boundary states for Gepner models, Nucl.Phys. B588 (2000) 110-148 (arXiv:hep-th/0003298)
(with emphasis on GSO projections)
-
Jürgen Fuchs, P. Kaste, Wolfgang Lerche, C. Lutken, Christoph Schweigert, J. Walcher, Boundary Fixed Points, Enhanced Gauge Symmetry and Singular Bundles on K3, Nucl.Phys.B598:57-72, 2001 (arXiv:hep-th/0007145)
See also
-
Andreas Recknagel, Volker Schomerus, D-branes in Gepner models, Nucl.Phys. B531 (1998) 185-225 (arXiv:hep-th/9712186)
-
Volker Braun, Sakura Schafer-Nameki, D-Brane Charges in Gepner Models, J. Math. Phys. 47 (2006) 092304 (arXiv:hep-th/0511100)
Discussion of permutation D-branes for Gepner models, via boundary conformal field theory, includes
- Håkon Enger, Andreas Recknagel, Daniel Roggenkamp, Permutation branes and linear matrix factorisations, JHEP0601:087, 2006 (arXiv:hep-th/0508053)
Gepner model orientifolds:
- Brandon Bates, Charles Doran, Koenraad Schalm, Crosscaps in Gepner Models and the Moduli space of T2 Orientifolds, Advances in Theoretical and Mathematical Physics, Volume 11, Number 5, 839-912, 2007 (arXiv:hep-th/0612228)
Specifically string phenomenology and the landscape of string theory vacua of Gepner model orientifold compactifications:
-
T.P.T. Dijkstra, L. R. Huiszoon, Bert Schellekens, Chiral Supersymmetric Standard Model Spectra from Orientifolds of Gepner Models, Phys.Lett. B609 (2005) 408-417 (arXiv:hep-th/0403196)
-
T.P.T. Dijkstra, L. R. Huiszoon, Bert Schellekens, Supersymmetric Standard Model Spectra from RCFT orientifolds, Nucl.Phys.B710:3-57,2005 (arXiv:hep-th/0411129)
-
Fernando Marchesano, Bert Schellekens, Timo Weigand, Sec. 4 of: D-brane and F-theory Model Building [arXiv:2212.07443]
Last revised on May 29, 2024 at 06:39:15. See the history of this page for a list of all contributions to it.